Let me start us off with a little warm up. When you look at this picture, what do you notice? Hold onto what you notice until the end.
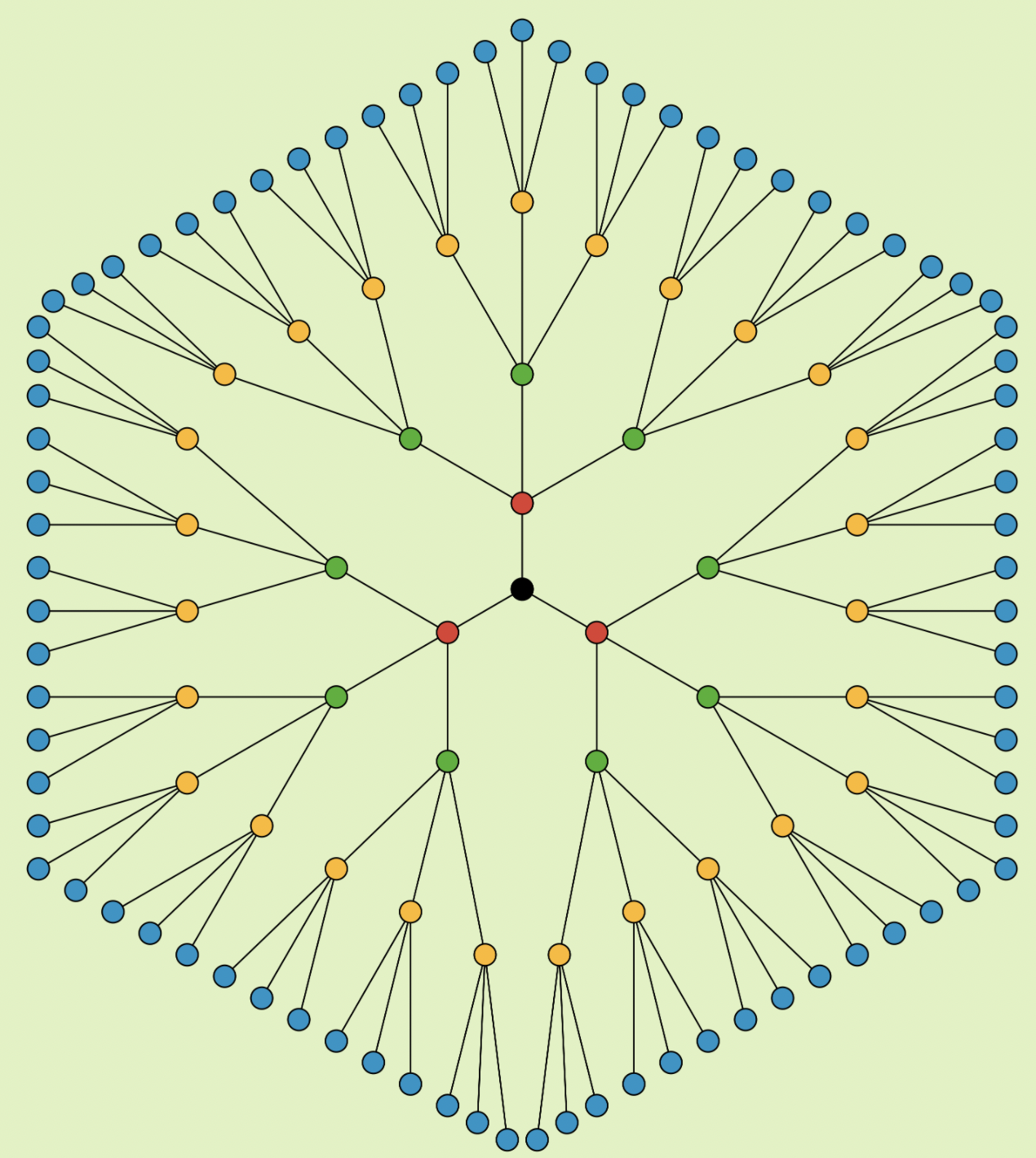
(Beckmann, 2018)
This was a warm up that I used during the past semester in my Mathematics for Elementary Teachers (MFET) classes. This image was on a Jamboard. Students provided their thoughts via sticky notes about what they noticed. Maybe you’re thinking, “yeah that works for Math for Elementary teachers but…” I also used this as a warm up for my Trigonometry class with similar results and will continue to use it (and other “what do you notice”) activities in every math class I teach. Why? Because what happens in MFET should NOT stay in MFET.
What is MFET?
Mathematics for Elementary Teachers is the course (or for most, course sequence) that future elementary teachers must take as a part of their preparation and certification/licensure. State requirements vary. In Illinois, the two courses are required for all “pre-service” teachers. The courses exist at both community colleges and four-year schools. Mathematics for Elementary Teachers is intended to be a content course, essentially with all of the math content that future K-8 teachers would need to know for their future teaching. But separating content from methods is not always possible (nor appropriate), and content knowledge alone is necessary but insufficient for teaching (Shulman, 1987; Ball, Thames and Phelps, 2008). Speaking from my own experience, there have been a number of local collaborative efforts around these courses in addition to this fantastic AMAYTC Teacher Preparation committee, allowing for us to compare our own balancing of content and methods.
And what happens in MFET?
If you’ve never had the pleasure of teaching it, first of all, you’re missing out. Second, think about all of the “stuff” that we do with respect to numbers, operations and geometry. The foundations for them came from our time as pre-K through 8th grade students. As math faculty, we ask why, but when we were students did we? One way to think of MFET is as a place to revisit why.
With respect to numbers, operations, geometry, probability, statistics and algebra.
MFET…
- answers the “why” questions.
- gets us thinking about student (mis)understandings.
- helps us to see the wide variety of methods, usually beyond what we experienced as students.
- is a deep dive into the origins of things that we take for granted, but are rich in their own right.
For example, think about multi-digit multiplication. Take a moment to multiply 25 x 40. How did you do it? Why does what you did work? What errors might students make when using paper-and-pencil or mental strategies? Could you figure out another way? Is the method that you used generalizable or specific to one or both factors? For instance, would your method work for 24 x 40 or 25 x 41? Perhaps there’s a modification you could make to your method, or maybe knowing a bit more about what is actually happening “behind the scenes” when we multiply is all we need. And it’s no coincidence that most of the methods used to multiply above are necessary in understanding how to multiply polynomials.
The previous paragraph is meant to give you a glimpse into what happens in an MFET class.
But how does that apply to classes that are not MFET?
I have been teaching MFET for about 16 years. I was asked to teach the course my first semester because I had two years teaching 6th grade (which was definitely enough 😉).
In the beginning, I really did think of MFET as something entirely different from the other courses I was teaching. But as the years have passed, I’ve noticed that much of what I do in other classes has been heavily influenced by my time teaching MFET. The Math for Elementary Teachers courses have made me a better teacher. Not only can I calculate more quickly, which is fun when in front of a class with an itch to show off, but MFET has also gotten me thinking about what our students have experienced prior to ending up in our classes. This is especially useful when teaching students in developmental courses where arithmetic is a part of the curriculum. I feel more prepared when they use strategies that differ from mine. I also feel more prepared with fundamental ideas. Consider graphing a function. In addition to evaluating the function, think about what we often take for granted: the choices of x values, the labeling of the axes and the intervals of the function that we care about. When graphing a cosine function, knowing how to subdivide an interval into 4 equal parts is very useful to find the “nice” points of the function. Partitioning is really just an application of fraction representation. We’re taking the whole and breaking it into four equal parts. Whether the whole is one or 2π does not change the fact that we’re breaking it into four equal parts.
MFET involves visualization. But visualization should happen everywhere, even for content that we may think should be strictly numerical or algebraic. I have been amazed over the years at the number of students who are surprised by me drawing out fraction arithmetic ideas. In our introduction to college mathematics courses, number sense is the first unit. Students who have anxiety about arithmetic (usually fractions and negative numbers) or who have been away from school mathematics for a while always appreciate how the visuals help them to understand why things work, like common denominators when adding/subtracting fractions, whether the visuals are pizzas or a number lines.
MFET involves collaboration and active learning. In the early part of my career, I thought that utilizing these methods in other courses that appeared more rigorous would be a bad idea. But with age and experience, I have listened to what MFET has taught me. Why should I reserve the most engaging parts of my practice for my MFET classes? In MFET, I tried more than every other course to model good math teaching so that students could take those ideas with them into their future practice. I have also been more experimental in my teaching in those courses. But good teaching is good teaching and taking risks shouldn’t be course dependent. Discussions about numbers through math talks (like the start of this post), role playing opportunities for students to teach each other or correct fictitious students’ work, using movement and manipulatives to engage more senses in their learning are all things that happen in MFET.
MFET involves more than procedures. Students are often surprised by the number of ways to solve a problem. They can also be resistant to seeing problems solved in ways that vary from their way. Students may begin a class with the mentality that the answer is more important than the way they got to the answer or why that way makes any sense. Imagine a procedure in one of the classes you teach. Is the goal for students to master the procedure or to understand the procedure? Is there a difference? In MFET, all procedures are demystified. Students should leave the course having few doubts about why anything works, especially with respect to arithmetic. They should also leave curious.
If these sound like things that you do or would like to do in your courses, then perhaps there is more in common between MFET and your courses than you may have previously thought.
So what did you notice up above?
Maybe you noticed something having to do with rotational symmetry. Maybe you noticed something more numerical, perhaps related to powers of 3. Feel free to reply with something you noticed and while you’re replying... if you teach MFET and other courses like me and most others in our teaching preparation committee, what doesn’t stay in MFET for you?
And if you’re not a part of it already, join AMATYC’s Teacher Preparation Committee!
P.S.
Here’s a shameless plug from my talk about MFET at this past AMATYC conference.
https://my.amatyc.org/viewdocument/the-professor-goes-to-schooland
References
Beckmann, S. (2018). Mathematics for elementary teachers, with activities.
Ball, D., Thames, M. H., & Phelps, G. (2008). Content Knowledge for Teaching: What Makes It Special? Journal of Teacher Education, 59(5), 389–407. https://doi.org/10.1177/0022487108324554
Shulman, L. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1), 1-22.